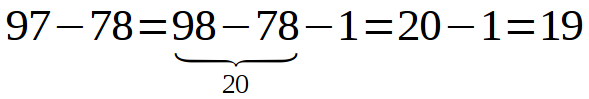
PhDr. Mgr. Jeroným Klimeš, Ph.D. 2017-01-13
Odčítání přes desítku (např. 97-78) je vždy pro děti složité, proto je třeba vždy vyzkoušet vícero metod a najít tu, která dětem vyhovuje. Synovi Erlanovi jsem teď ukazoval tuto metodu, zkuste ji, třeba bude Vašim dětem taky vyhovovat.
Zkusím to říci jako souvislé vyprávění:
Mám spočítat:
97-78
Hmm, to se blbě počítá. Mnohem lépe by se mi počítalo:
98-78
To by bylo dvacet, ale to by mi musel kamarád Martin půjčit jednu korunu. Dobrá, tak si ji na chvíli půjčím, ale pak ji musím vrátit (-1):
97 - 78 je tedy jako
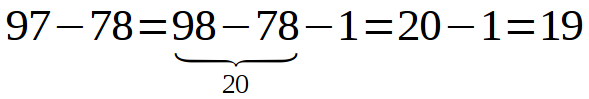
Stejně tak u jiných výpočtů:
81 - 56
No, lépe by se mi počítalo
86 - 56
Ale to by mi Martin musel půjčit bůra. Já bych mu ho ale vzápětí vrátil.
Metoda Mgr. Ing. Miroslava Skaly
97 Kč - 78 Kč počítám, jako kdybych měl číšníkovi zaplatit 78 Kč a z nějakého důvodu jsem mu namísto toho vysypal celou peněženku a tam bylo 97 Kč. Kolik mi má vrátit?
V prvním kroku: odhadnu, že přibližně by mi měl vrátit 20 Kč (počítám 90-70=20). Tímto způsobem se mimochodem bráním takovým těm fintám, kdy číšník by mi vrátil sice na koruny přesně, ale až doma bych zjistil, že mně ošidil "přesně o padesátikorunu". Jak dříve někteří mazaní číšníci dělávali.
Ve druhém kroku: mám-li při placení ještě chvilku času, tak si uvědomím, jaké číslice vlastně byly na místě jednotek. Bylo tam 7 Kč - 8 Kč = (-1 Kč), takže číšník mi vrátí fakticky o 1 Kč méně.
Tedy nedostanu 20 Kč, nýbrž 19 Kč.
Poznámka JK
Jestli jsem to dobře pochopil, tak napřed dítě má odečíst desítky:
90-70 = 20
Pak jednotky:
7-8=-1
Nakonec dohromady:
20-1=19
Ještě dodatečně mě napadlo, že v obchodech se prodavači vyhybají odčítání tím, že vrací dopočítáváním do plné ceny:
Jídlo stálo 78 a zákazník platil stovkou, tedy musím mu dát 2 Kč, to bude 80 Kč, pak ještě dvacku.
78 + 2 = 80 ...+20=100
Tady by to bylo asi tak, že poctivý číšník by si vzal 80, zbytek by mi vrátil, že to nepotřebuje, pak by mi ještě vrátil 2 Kč.
78 + 2 =80 ...+10=90 ...+5 +2=97
Jsou každopádně dvě otázky: Co je rychlejší? Co je méně chybové?
Je pravda, že jak se čísla převedou na peníze, tak děti dělají méně chyb.