Bagr nad přeponou se rovná součtu bagrů nad oběma odvěsnami, aneb
Pythagorova věta a² + b² = c²

PhDr. Mgr. Jeroným Klimeš, Ph.D. 2017-02-11

Když jsem byl na škole, tak se nám dala Pythagorova věta k věření. Nikdo se nesnažil nám vysvětlit, jak k tomu Pythagoras dospěl. To mě ale zajímalo, tak jsem se pídil po důkazu. Řekli mi příklad: strany 3, 4, 5 tvoří takový trojúhelník. To je ovšem jen příklad - jeden z možných případů. Jak mohl Pythagoras dospět k závěru, že to tak platí pro každý pravoúhlý trojúhelník. Hledal jsem, hledal a nakonec mě překvapilo, že ten důkaz je stejně jednoduchý jako geniální.

Vezměme to po pořádku. Mějme tento červený pravoúhlý trojúhelník ABC.

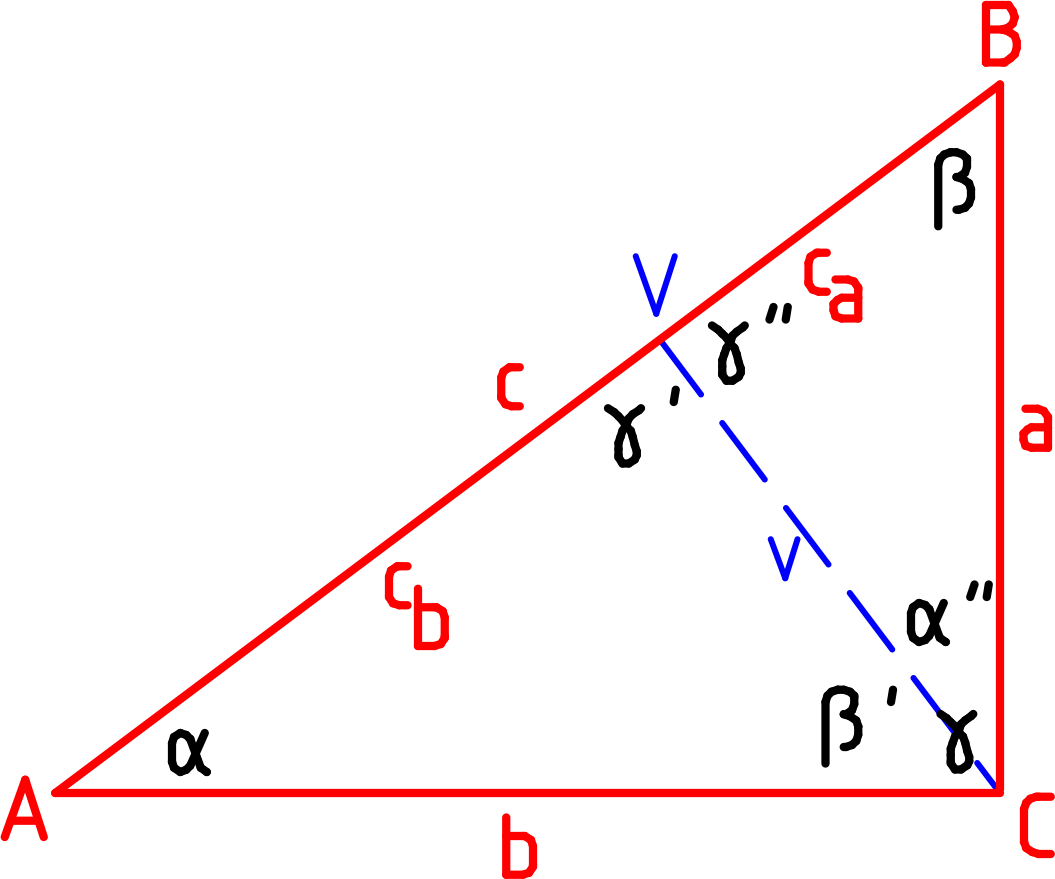
Pythagoras vyšel z faktu, který mi nebyl na první pohled zřejmý. Když si nakreslíme do tohoto trojúhelníku výšku v, rozdělí ta trojúhelník ABC na dva menší trojúhelníky (AVC a VBC). Ty mají ovšem jednu zajímavou vlastnost - jsou si podobné jak vzájemně, tak jsou podobné se samotným trojúhelníkem ABC, tzn. mají stejné úhly α, β, γ, neboť platí

γ = α + β = 90°

α + β + γ = 180°

Máme tedy tři podobné trojúhelníky: červený = modrý + zelený. Stačí je překlopit a pootočit a můžeme je naskládat přes sebe:

Jestliže jsou si takto podobné, musejí jejich strany být ve stejném poměru, tzn. musejí platit následující úměry.

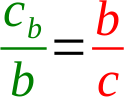
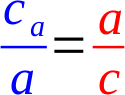
Barvy odpovídají jednotlivým trojúhelníkům. Vždy přilehlá odvěsna ku přeponě v prvním trojúhelníku se musí rovnat poměru stejných stran v druhém trojúhleníku - jednou u úhlu α, podruhé u úhlu β.

Ty upravíme na:

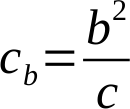
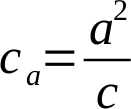
Tyto dva vzorce dáme pod sebe, sečteme a mírně upravíme:

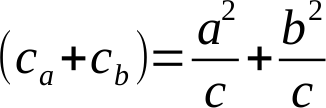
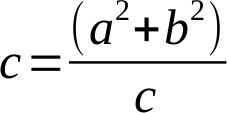
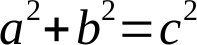
A máme Pythagorovu větu! QED

Grafický důkaz

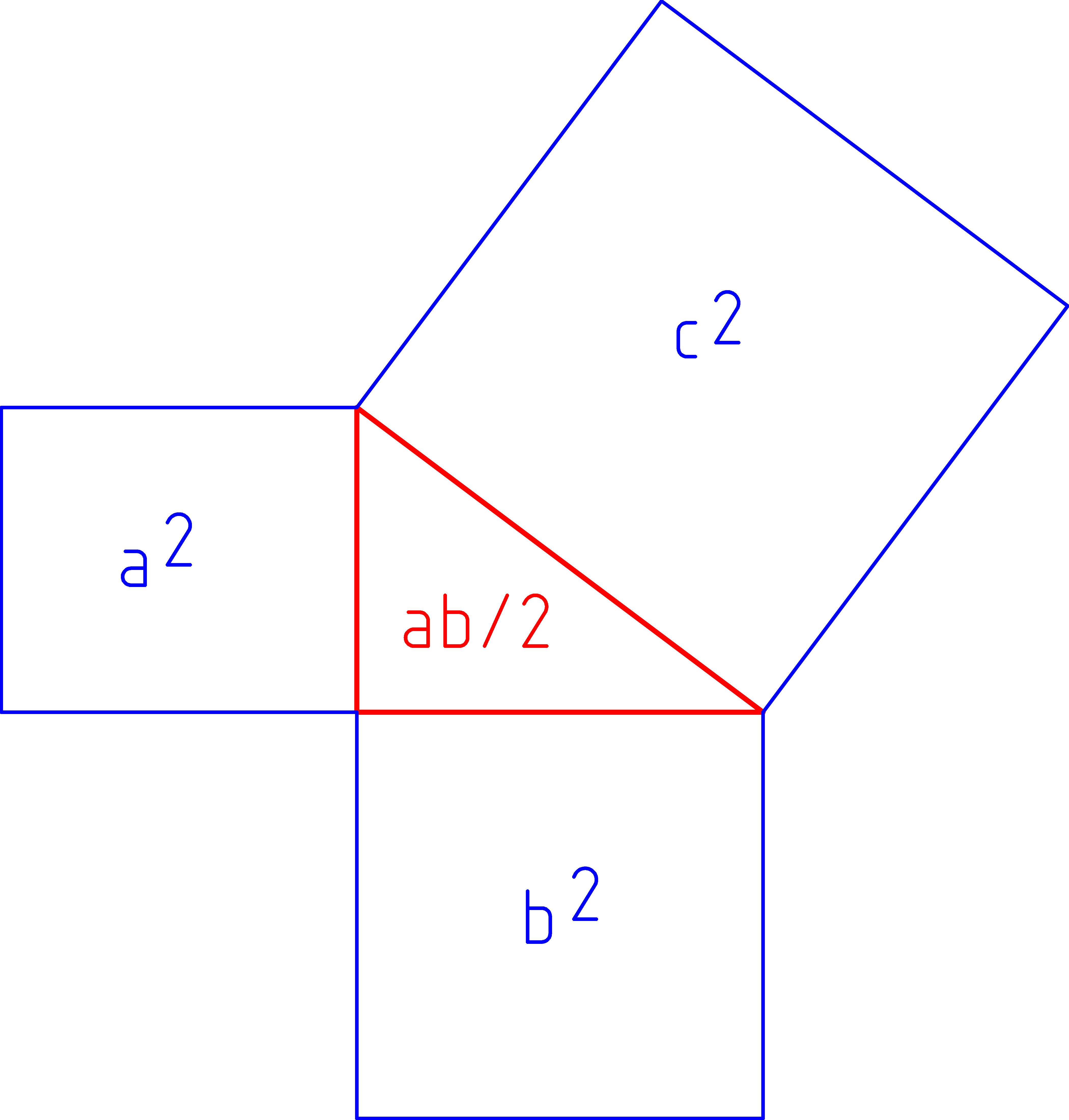
Na Wikipedii mají ještě grafický důkaz, který jsem prve neznal. Pokud se ale nepletu, Pythagoras sám vycházel z předchozích úměr a z výšky.

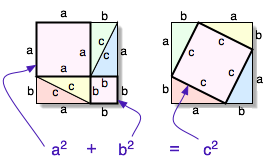
a) Nakreslíme dva stejné čtverce o straně stejně dlouhé jako součet obou odvěsen trojúhelníka (a+b)

b) Na jeden vyneseme úsečky dokola v pořadí "ab ab ba ba"

a na druhý v pořadí "ab ab ab ab"

c) Vzniklé střední body propojíme tak, aby vznikly čtverce (a², b², c²).

d) Obdélníky rozřízneme úhlopříčkou na trojúhelníky.

Takto jsme získali po čtyřech exemplářích zkoumaného trojúhelníku (abc) v každém velkém čtverci.

Oba velké čtverce jsou stejně velké, proto když od každého čtverce odečteme čtyři stejné trojúhelníky, musí nám zbýt stejná plocha, i když má jiný tvar. A to je Pythagorova věta, která měla být dokázána. QED

Triviální rozšíření, které ovšem málokdo zná

Pythagorovu větu můžeme vynásobit jakoukoli konstantou: k.a² + k.b²= k.c². Místo čtverců pak dostaneme jiný obrazec o ploše k.c². Například pokud je konstanta k=π/4, resp. k=π/8, pak dostaneme modifikovanou Pythagorovu větu: (Půl)kruh nad přeponou se rovná součtu (půl)kruhů na oběma odvěsnami.

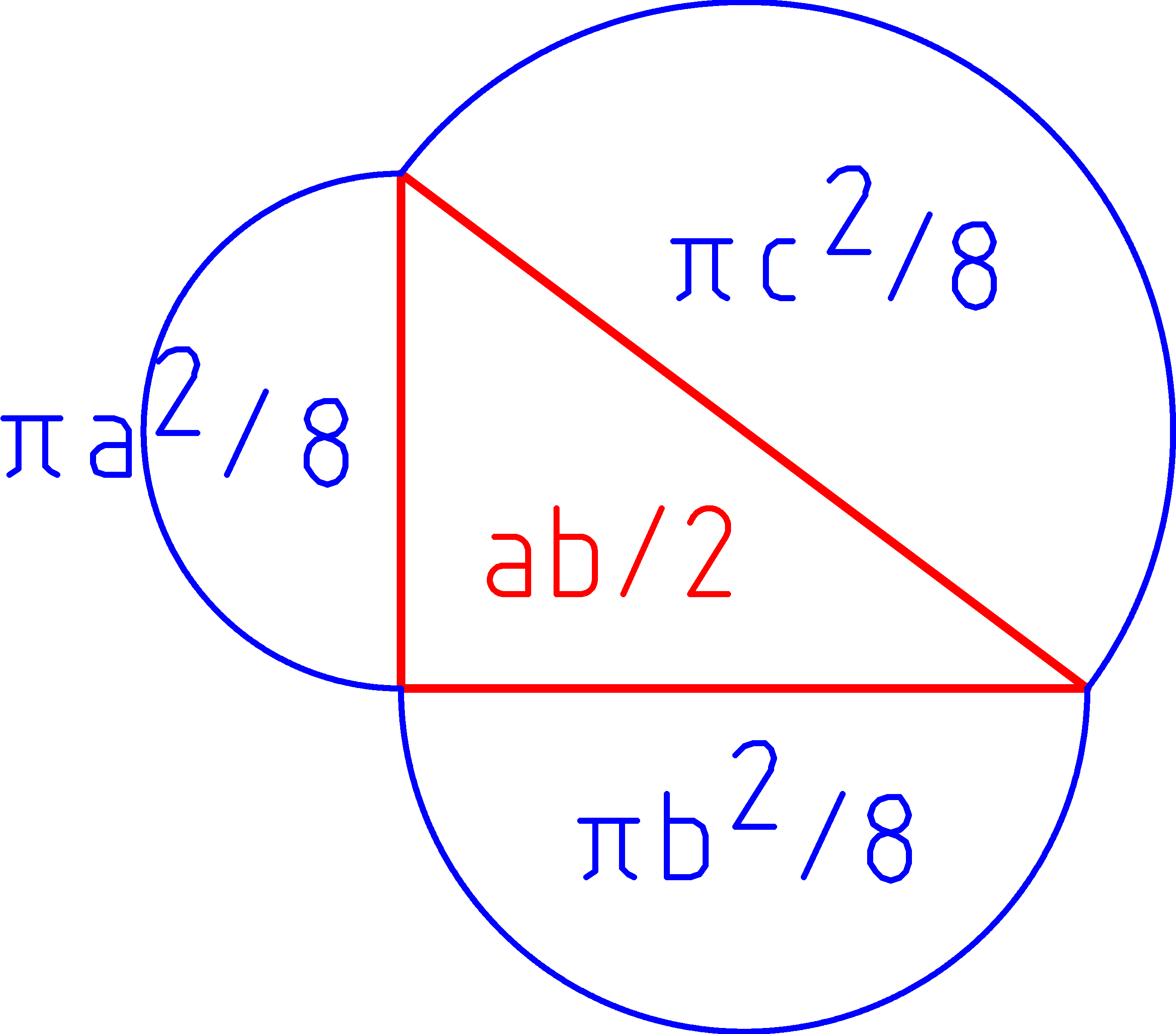
Podobně:
Plocha kosočtverce, smajlíku, domečku, resp. bagru nad přeponou se rovná součtu kosočtverců, smajlíků, domečků, resp. bagrů nad oběma přeponami.

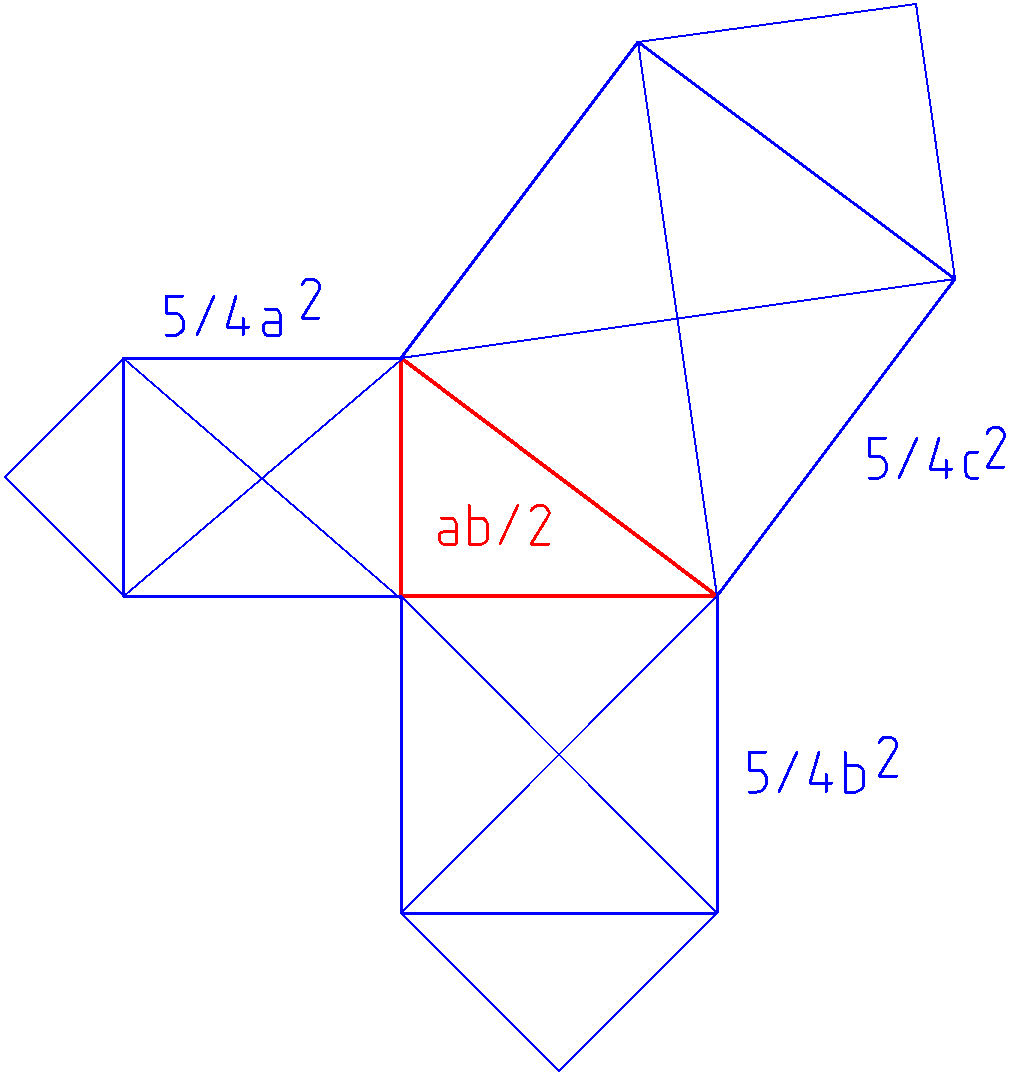
Nevím, jak vy, ale cítím, že můj život byl ochuzen tím, že mi toto bagrové moudro na základní škole odepřeli!

Pythagorova věta v psychologii

Je zřejmé, že Pythagorova věta má široké pole využití. Málokdo by však čekal, že ji již mnoho let zdárně využívám i v psychologii jako test toho, zda má člověk rozchod za sebou. Test je to jednoduchý: Rozchod máte za sebou, když je vám bývalý partner asi tak lhostejný jako Pythagoras:

Pokračování Hippokratovy měsíčky